Back to Kemp Acoustics Home




Next: Numerical implementation issues
Up: Acoustic pulse reflectometry
Previous: Input impedance from the
Contents
Layer peeling bore reconstruction
We now want to analyse the input impulse response to find out the reflection
coefficients (and therefore the changes in cross-section) at each step
along the bore. This will enable us to reconstruct the bore profile.
Bore reconstruction was first performed using the algorithm developed by
Ware and Aki [7] as reviewed in [6]. Since losses
cannot be incorporated in the Ware Aki algorithm, we will instead use
the lossy reconstruction method developed by
Amir et al. [17] as used by Sharp [6,19,20].
Consider a junction between two infinite tubes. If a pressure wave is incident
from negative infinity and no wave is incident from positive infinity, then
the ratio of the backward and forward going waves is given by the reflection
coefficient of equation (2.20).
Going back to the general case of an object attached to the source tube
of a reflectometer from figure 5.1, at the first time step
(ie. when the forward going pulse arrives at the input plane), there cannot
be any backward going waves on surface 2.
The ratio of the first term in the
reflection sequence (or input impulse response) and the first term in the
input sequence (which is unity) is therefore equal to the reflection
coefficient from equation (2.20). We will
label this reflection coefficient as 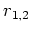 . The subscripts indicate that
this reflection coefficient is for reflection from the discontinuity between
surfaces 1 and 2 when waves are incident from the surface 1 side only.
. The subscripts indicate that
this reflection coefficient is for reflection from the discontinuity between
surfaces 1 and 2 when waves are incident from the surface 1 side only.
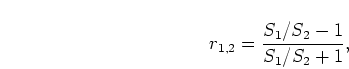 |
(5.8) |
![\begin{displaymath}
r_{1,2} = \frac{p_{-}^{(1)}[0T]}{p_{+}^{(1)}[0T]} = iir[0T],
\end{displaymath}](img474.png) |
(5.9) |
where we have labelled the surface area of surface 1 as 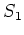 and the surface
area of surface 2 as
and the surface
area of surface 2 as 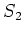 . Now
. Now 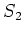 follows from
follows from 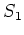 and
and 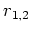 by
rearranging equation (5.8):
by
rearranging equation (5.8):
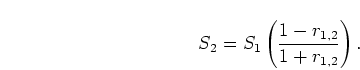 |
(5.10) |
Now we know the cross-section on section 2, we will proceed to calculate the
forward and backward going time sequences there.
The forward going wave on section 2 is equal to the sum of the transmission
of the forward going wave on section 1 and reflection of the backward going
wave on section 2. Similarly, the backward going wave on section 1 is equal to
the sum of the transmission of the backward going wave on section 2 and the
reflection of the forward going wave on section 1. It can be expressed in
matrix notation as follows:
![\begin{displaymath}
\left( \begin{array}{c} p_{+}^{(2)}[nT] \\ p_{-}^{(1)}[nT] \...
...ay}{c} p_{+}^{(1)}[nT] \\ p_{-}^{(2)}[nT] \end{array} \right).
\end{displaymath}](img476.png) |
(5.11) |
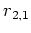 gives the reflection coefficient from the discontinuity between
surfaces 2 and 1 when waves are incident from the surface 2 side only:
gives the reflection coefficient from the discontinuity between
surfaces 2 and 1 when waves are incident from the surface 2 side only:
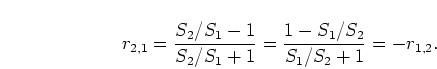 |
(5.12) |
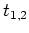 gives the transmission coefficient from the discontinuity between
surfaces 1 and 2 when waves are incident from the surface 1 side only.
From equation (2.21) this is
gives the transmission coefficient from the discontinuity between
surfaces 1 and 2 when waves are incident from the surface 1 side only.
From equation (2.21) this is
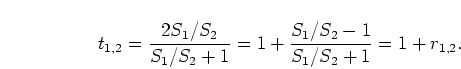 |
(5.13) |
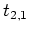 gives the transmission coefficient from the discontinuity between
surfaces 2 and 1 when waves are incident from the surface 2 side only:
gives the transmission coefficient from the discontinuity between
surfaces 2 and 1 when waves are incident from the surface 2 side only:
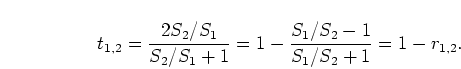 |
(5.14) |
We may rearrange the simultaneous equations in equation
(5.11) to give
the travelling waves on the right of the discontinuity in terms of the
travelling waves on the left of the discontinuity:
![\begin{displaymath}
\left( \begin{array}{c} p_{+}^{(2)}[nT] \\ p_{-}^{(2)}[nT] \...
...ay}{c} p_{+}^{(1)}[nT] \\ p_{-}^{(1)}[nT] \end{array} \right).
\end{displaymath}](img483.png) |
(5.15) |
This equation is performed for all values of  from
from 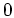 to
to 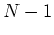 .
For the current situation, the forward going sequence on surface 1 is an
impulse,
.
For the current situation, the forward going sequence on surface 1 is an
impulse,
![$p_{+}^{(1)}[nT] = \delta[nT]$](img484.png) , and the backward going pressure
sequence on surface 1 is the input impulse response,
, and the backward going pressure
sequence on surface 1 is the input impulse response,
![$p_{-}^{(1)}[nT] = iir[nT]$](img485.png) . Notice that
. Notice that
![\begin{displaymath}
p_{-}^{(2)}[0] = -r_{1,2} \times \delta[0] + 1 \times iir[0] = 0
\end{displaymath}](img486.png) |
(5.16) |
as no reflections return from surface 3 until 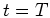 .
.
The forward travelling pressure sequence, at the right
hand side of the cylindrical section, will be found simply by adding a
delay time of 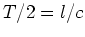 to the forward going wave on the left, to account
for the time taken to travel a distance of
to the forward going wave on the left, to account
for the time taken to travel a distance of 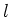 .
.
![\begin{displaymath}
p_{+}^{(3)}\left[\left(n+\frac{1}{2}\right) T\right] = p_{+}^{(2)}[nT].
\end{displaymath}](img489.png) |
(5.17) |
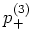 is therefore known at
is therefore known at 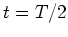 and in steps of
and in steps of 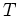 up to
up to
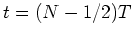 .
.
The backward travelling wave at surface 3 is found by subtracting a delay of
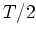 from the backward travelling wave at surface 2.
from the backward travelling wave at surface 2.
![\begin{displaymath}
p_{-}^{(3)}\left[\left(n-\frac{1}{2}\right) T\right] = p_{-}^{(2)}[nT].
\end{displaymath}](img495.png) |
(5.18) |
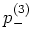 is therefore known at
is therefore known at 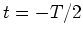 and in steps of
and in steps of 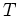 up to
up to
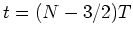 .
Notice that there is no backward going wave on surface 3 until
.
Notice that there is no backward going wave on surface 3 until 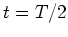 :
:
![\begin{displaymath}
p_{-}^{(3)}[-T/2] = p_{-}^{(2)}[0] = 0
\end{displaymath}](img499.png) |
(5.19) |
since no waves reach surface 3 until this time.
The ratio of the backward and forward travelling waves at
surface 3, at time 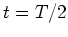 , is equal to the reflection coefficient
, is equal to the reflection coefficient 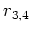 since this corresponds to a primary reflection.
since this corresponds to a primary reflection.
![\begin{displaymath}
r_{3,4} = \frac{p_{-}^{(3)} [T/2]}{p_{+}^{(3)}[T/2]}.
\end{displaymath}](img501.png) |
(5.20) |
Subsections
Back to Kemp Acoustics Home




Next: Numerical implementation issues
Up: Acoustic pulse reflectometry
Previous: Input impedance from the
Contents
Jonathan Kemp
2003-03-24
![]() . The subscripts indicate that
this reflection coefficient is for reflection from the discontinuity between
surfaces 1 and 2 when waves are incident from the surface 1 side only.
. The subscripts indicate that
this reflection coefficient is for reflection from the discontinuity between
surfaces 1 and 2 when waves are incident from the surface 1 side only.
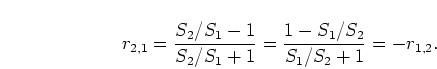
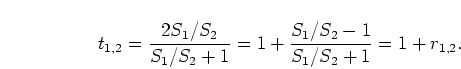
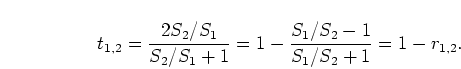
![\begin{displaymath}
p_{-}^{(2)}[0] = -r_{1,2} \times \delta[0] + 1 \times iir[0] = 0
\end{displaymath}](img486.png)
![]() to the forward going wave on the left, to account
for the time taken to travel a distance of
to the forward going wave on the left, to account
for the time taken to travel a distance of ![]() .
.
![]() from the backward travelling wave at surface 2.
from the backward travelling wave at surface 2.
![\begin{displaymath}
p_{-}^{(3)}[-T/2] = p_{-}^{(2)}[0] = 0
\end{displaymath}](img499.png)
![]() , is equal to the reflection coefficient
, is equal to the reflection coefficient ![]() since this corresponds to a primary reflection.
since this corresponds to a primary reflection.