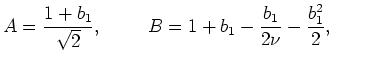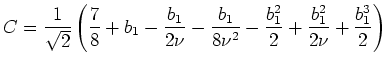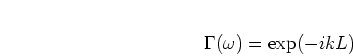Back to Kemp Acoustics Home



Next: Apparatus
Up: Layer peeling bore reconstruction
Previous: Numerical implementation issues
Contents
Losses
So far the effect of propagating waves down each cylindrical section
is simply represented by a delay of 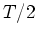 , therefore ignoring losses.
A way of including losses in the layer peeling algorithm has been presented
by Amir et al. [18].
, therefore ignoring losses.
A way of including losses in the layer peeling algorithm has been presented
by Amir et al. [18].
The frequency domain formula for losses associated with
propagation of plane acoustic waves down a tube of length 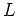 , due to Keefe
[54], forms the basis of the inclusion of losses in the layer
peeling algorithm. The effect of losses are characterised by the complex
wavenumber,
, due to Keefe
[54], forms the basis of the inclusion of losses in the layer
peeling algorithm. The effect of losses are characterised by the complex
wavenumber, 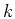 :
:
 |
(5.25) |
where 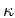 is the frequency dependent attenuation due to boundary layer
effects, while
is the frequency dependent attenuation due to boundary layer
effects, while
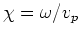 is the ratio of the angular frequency and
the phase velocity for propagation of sound
along the tube. They are given by Keefe [54] as:
is the ratio of the angular frequency and
the phase velocity for propagation of sound
along the tube. They are given by Keefe [54] as:
![\begin{displaymath}
\chi = \frac{\omega}{c}\left[
1 + \frac{A}{r_v} - \frac{C}{r...
... [
\frac{A}{r_v} + \frac{B}{r_v^2} + \frac{C}{r_v^3}
\right ]
\end{displaymath}](img521.png) |
(5.26) |
where the normalised boundary layer thickness is
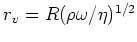 and depends on the tube radius,
and depends on the tube radius,
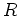 .
. 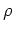 is the density and
is the density and 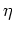 is the coefficient of
viscosity of air. The coefficients
is the coefficient of
viscosity of air. The coefficients 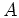 ,
, 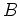 and
and 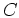 are also functions of the
thermodynamic constants of air:
are also functions of the
thermodynamic constants of air:
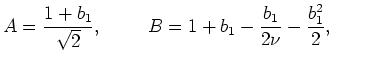 |
|
|
|
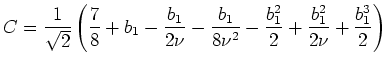 |
|
|
(5.27) |
with
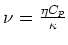 where
where 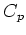 is the specific heat of air
at constant pressure,
is the specific heat of air
at constant pressure, 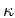 is the thermal conductivity of air and
is the thermal conductivity of air and
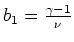 where
where 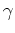 is the ratio of the specific
heats of air. Temperature dependent values of the thermodynamic
constants of air due to Keefe [54] are provided in
table 5.1. The imaginary part of the wavenumber responsible
for attenuation is then
is the ratio of the specific
heats of air. Temperature dependent values of the thermodynamic
constants of air due to Keefe [54] are provided in
table 5.1. The imaginary part of the wavenumber responsible
for attenuation is then
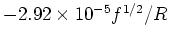 for
for 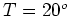 ,
which agrees with the value quoted in Kinsler et al. [40]
to within 1% and differs from the plane wave value from the multimodal
losses theory due to Bruneau [44] by 3%.
,
which agrees with the value quoted in Kinsler et al. [40]
to within 1% and differs from the plane wave value from the multimodal
losses theory due to Bruneau [44] by 3%.
Table 5.1:
Thermodynamic constants
|
|
This means that the resulting transmission coefficient is:
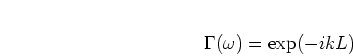 |
(5.28) |
There are numerical difficulties which arise when trying to use this as a
filter within the bore reconstruction algorithm.
These issues are treated in detail by Amir et al. [18].
Back to Kemp Acoustics Home



Next: Apparatus
Up: Layer peeling bore reconstruction
Previous: Numerical implementation issues
Contents
Jonathan Kemp
2003-03-24
![]() , due to Keefe
[54], forms the basis of the inclusion of losses in the layer
peeling algorithm. The effect of losses are characterised by the complex
wavenumber,
, due to Keefe
[54], forms the basis of the inclusion of losses in the layer
peeling algorithm. The effect of losses are characterised by the complex
wavenumber, ![]() :
:

![\begin{displaymath}
\chi = \frac{\omega}{c}\left[
1 + \frac{A}{r_v} - \frac{C}{r...
... [
\frac{A}{r_v} + \frac{B}{r_v^2} + \frac{C}{r_v^3}
\right ]
\end{displaymath}](img521.png)