Back to Kemp Acoustics Home




Next: Losses
Up: Layer peeling bore reconstruction
Previous: Layer peeling bore reconstruction
Contents
In terms of numerical implementation of the algorithm, the time domain
pressure travelling waves are stored in vectors with elements referred to
by an index (which we shall call 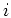 ) which runs from 1 to
) which runs from 1 to 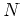 . Care must
be taken over
what time is represented by the index. On surfaces 1 and 2 we know
the pressure at
. Care must
be taken over
what time is represented by the index. On surfaces 1 and 2 we know
the pressure at 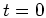 ,
, 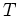 ,
, 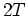 , ...,
, ..., 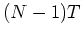 so the
so the 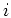 th element of
the vector in the numerical implementation therefore corresponds to the
pressure at time
th element of
the vector in the numerical implementation therefore corresponds to the
pressure at time 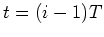 .
.
Equations (5.9) and (5.15) are
then simply
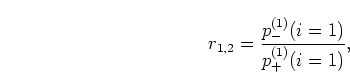 |
(5.21) |
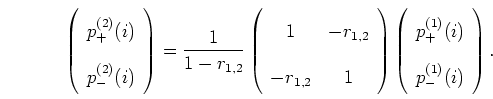 |
(5.22) |
The forward going pressure wave on surface 3 is sampled
at 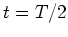 ,
, 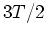 ,
, 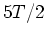 , ...,
, ...,  and the
and the 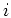 th element refers to
the time
th element refers to
the time 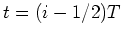 . Comparison with equation (5.17) then yields
. Comparison with equation (5.17) then yields
 |
(5.23) |
For the pressure on surface 3, we know the backward going
pressure at 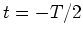 ,
, 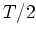 ,
, 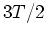 , ...,
, ..., 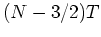 . At
. At 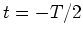 the
backward going
pressure is zero, so we only need to carry on using the non-zero pressures
at
the
backward going
pressure is zero, so we only need to carry on using the non-zero pressures
at 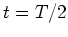 ,
,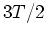 , ...,
, ..., 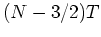 . The
. The 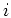 th element refers to the
time at
th element refers to the
time at 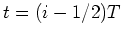 . Comparison with equation (5.18) gives
. Comparison with equation (5.18) gives
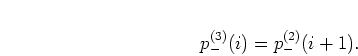 |
(5.24) |
The pressure waves
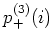 and
and
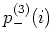 are then the
forward going and backward going sequences for the left hand side of the
junction at surface 3. We have therefore peeled off the first layer
in the object. Equations (5.21) to (5.24)
can then be used to peel off the next layer.
First the primary reflection coefficient for the junction from surface 3
to surface 4 is calculated, then the forward and backward travelling
waves on surface 4 are obtained and
then the delay for travel along the cylinder to next discontinuity is added.
The algorithm repeats as necessary, peeling off successive layers in the
object, calculating the new cross-section using
equation (5.10) each time.
are then the
forward going and backward going sequences for the left hand side of the
junction at surface 3. We have therefore peeled off the first layer
in the object. Equations (5.21) to (5.24)
can then be used to peel off the next layer.
First the primary reflection coefficient for the junction from surface 3
to surface 4 is calculated, then the forward and backward travelling
waves on surface 4 are obtained and
then the delay for travel along the cylinder to next discontinuity is added.
The algorithm repeats as necessary, peeling off successive layers in the
object, calculating the new cross-section using
equation (5.10) each time.
Back to Kemp Acoustics Home




Next: Losses
Up: Layer peeling bore reconstruction
Previous: Layer peeling bore reconstruction
Contents
Jonathan Kemp
2003-03-24
![]() ) which runs from 1 to
) which runs from 1 to ![]() . Care must
be taken over
what time is represented by the index. On surfaces 1 and 2 we know
the pressure at
. Care must
be taken over
what time is represented by the index. On surfaces 1 and 2 we know
the pressure at ![]() ,
, ![]() ,
, ![]() , ...,
, ..., ![]() so the
so the ![]() th element of
the vector in the numerical implementation therefore corresponds to the
pressure at time
th element of
the vector in the numerical implementation therefore corresponds to the
pressure at time ![]() .
.
![]() ,
, ![]() ,
, ![]() , ...,
, ..., ![]() and the
and the ![]() th element refers to
the time
th element refers to
the time ![]() . Comparison with equation (5.17) then yields
. Comparison with equation (5.17) then yields