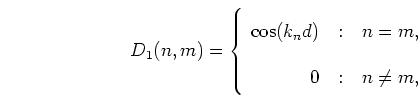Back to Kemp Acoustics Home




Next: Solutions for a cylinder
Up: Multimodal propagation in acoustic
Previous: Plane waves at a
Contents
The inclusion of higher modes in horn acoustics has been
studied recently [32,33,38,41,42].
In general, the
pressure and velocity in a cylinder can be expressed in terms of the
modes of the duct whose
amplitude patterns have  nodal circles and
nodal circles and 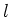 nodal diameters on a
circular cross-section where
nodal diameters on a
circular cross-section where 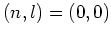 is the plane wave mode.
We are analysing axi-symmetric systems so we will treat axi-symmetric
(nodal circle) modes only. The pressure and volume velocity are then vectors
with a single subscript,
is the plane wave mode.
We are analysing axi-symmetric systems so we will treat axi-symmetric
(nodal circle) modes only. The pressure and volume velocity are then vectors
with a single subscript,  .
.
In the case of rectangular cross-section, the
modes of the duct will have an integer number of nodal lines parallel to the
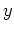 axis and an integer number of nodal lines parallel to the
axis and an integer number of nodal lines parallel to the 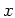 axis.
We will only treat systems that preserve symmetry about the central axis, so
only modes with an even number of nodal lines in both dimensions need to be
considered and the subscript
axis.
We will only treat systems that preserve symmetry about the central axis, so
only modes with an even number of nodal lines in both dimensions need to be
considered and the subscript 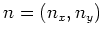 will be used where
there are
will be used where
there are 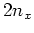 nodal lines parallel to the
nodal lines parallel to the 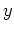 axis and
axis and 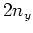 nodal lines
parallel to the
nodal lines
parallel to the 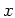 axis.
axis.
The pressure for each mode obeys the 3
dimensional wave equation:
 |
(2.22) |
Here  is the Laplacian operator which may be expressed as the sum
of the
is the Laplacian operator which may be expressed as the sum
of the 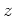 direction component and the component on the
direction component and the component on the 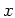 -
-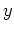 plane:
plane:
 |
(2.23) |
where 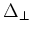 is given in Cartesian coordinates as
is given in Cartesian coordinates as
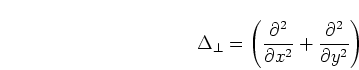 |
(2.24) |
and in cylindrical polars as
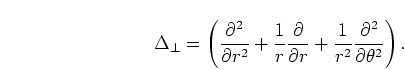 |
(2.25) |
The wave equation can be solved by expressing the pressure as a sum of
the contributions of the modes of the duct where each term is
the multiplication of the profiles along 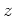 ,
, 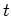 and the
and the 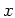 -
-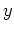 plane.
plane.
We can then solve the problem by separation of
variables ([43] pp.540-556).
From Pagneux et al. [32] the pressure and axial velocity are:
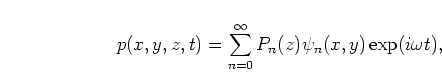 |
(2.26) |
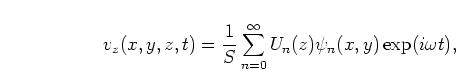 |
(2.27) |
where 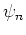 is the pressure profile on the
is the pressure profile on the 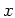 -
-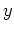 plane and
plane and 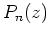 is the pressure profile of the
is the pressure profile of the  th mode along the length of the tube.
Similarly,
th mode along the length of the tube.
Similarly, 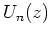 is the axial volume velocity profile of the
is the axial volume velocity profile of the
 th mode along the length of the tube.
th mode along the length of the tube. 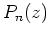 and
and 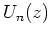 are in general
complex numbers to take phase into account.
Note that although it is convenient to refer to
are in general
complex numbers to take phase into account.
Note that although it is convenient to refer to 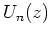 as the volume
velocity, the net volume velocity is
as the volume
velocity, the net volume velocity is 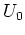 ; the other
entries are the amplitudes of the axial velocity distributions multiplied by
the surface area but have no net contribution to the volume
velocity [32].
; the other
entries are the amplitudes of the axial velocity distributions multiplied by
the surface area but have no net contribution to the volume
velocity [32].
Equation (2.26) gives the pressure as a series of terms, 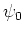 being unity, and so the
being unity, and so the 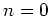 contribution represents plane wave propagation
while the other modes have a non-uniform pressure profile. Substituting
contribution represents plane wave propagation
while the other modes have a non-uniform pressure profile. Substituting
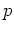 from equation (2.26) into the wave
equation (2.22) and dividing through by
from equation (2.26) into the wave
equation (2.22) and dividing through by 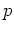 gives:
gives:
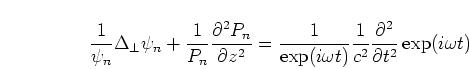 |
(2.28) |
Since each term in this equation is a function of a different variable, each
term must equal a constant.
The differentiation with respect to 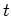 is straightforward giving
is straightforward giving
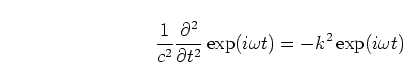 |
(2.29) |
with the eigenvalue 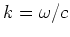 being the free space wavenumber.
Defining
being the free space wavenumber.
Defining 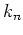 to be the wavenumber along
to be the wavenumber along 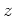 (commonly referred to as the
propagation factor):
(commonly referred to as the
propagation factor):
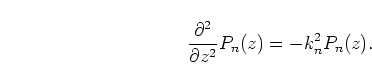 |
(2.30) |
The transverse term gives
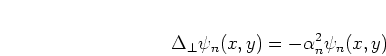 |
(2.31) |
with 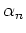 being the eigenvalue of the
being the eigenvalue of the  th mode. Physically
th mode. Physically 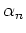 is the wavenumber in the
is the wavenumber in the 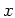 -
-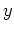 plane and is zero for plane wave propagation
and is positive and real for the modes which feature nodal lines or circles.
plane and is zero for plane wave propagation
and is positive and real for the modes which feature nodal lines or circles.
It then follows from equation (2.28) that the
wavenumbers follow the relation
 |
(2.32) |
The wavelength along 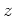 will be
will be
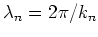 .
.
Note that in a pipe of uniform cross-section the solution of equation
(2.30) gives
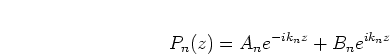 |
(2.33) |
To find the corresponding volume velocities we use the force equation
(2.4). The 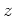 component of the velocity is
component of the velocity is
 |
(2.34) |
giving the corresponding axial volume velocity as
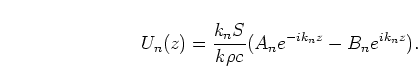 |
(2.35) |
We can note from this that the characteristic
impedance, defined to be the ratio of pressure and volume velocity of
forward travelling waves, also depends on the mode number,  . For plane
waves it was
. For plane
waves it was
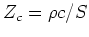 but for the
but for the  th mode this becomes:
th mode this becomes:
 |
(2.36) |
Assuming loss-less propagation 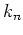 is positive and real above cut-off
point (
is positive and real above cut-off
point (
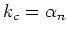 ) so the pressure varies sinusoidally along the
) so the pressure varies sinusoidally along the 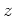 axis
with a wavelength of
axis
with a wavelength of
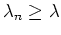 where
where
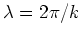 is the
free-space wavelength.
Below the cut-off point
is the
free-space wavelength.
Below the cut-off point 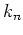 is negative and imaginary [42]
so the pressure will be exponentially damped. Calculation of
is negative and imaginary [42]
so the pressure will be exponentially damped. Calculation of 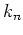 first requires calculation of
first requires calculation of 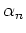 which in turn
depends on the boundary conditions in equation (2.31)
(and therefore on the geometry of the duct). It will
be treated for both lossy and non-lossy propagation in section
2.4.1 for ducts of circular cross-section and in section
2.4.2 for rectangular ducts.
which in turn
depends on the boundary conditions in equation (2.31)
(and therefore on the geometry of the duct). It will
be treated for both lossy and non-lossy propagation in section
2.4.1 for ducts of circular cross-section and in section
2.4.2 for rectangular ducts.
We have seen that plane waves travelling across a section of tube are only
reflected when the cross-section changes.
The plane wave pressure amplitude at any point in a uniform section of tube
may be obtained from a known plane wave pressure amplitude at a single point
simply by projection using equation (2.10). Each of the other modes of
the pipe will also
only be reflected where the cross-section changes and so may be treated
independently in a section of uniform cross-section. The wavenumber along
the 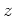 axis becomes
axis becomes 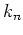 for the
for the  th mode and, as discussed earlier in the
section, the characteristic
impedance of the
th mode and, as discussed earlier in the
section, the characteristic
impedance of the  th mode is
th mode is
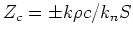 .
Projection of pressure and volume velocity complex amplitudes
of the
.
Projection of pressure and volume velocity complex amplitudes
of the  th mode then follow from equations (2.10) and (2.11).
th mode then follow from equations (2.10) and (2.11).
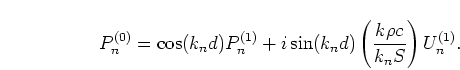 |
(2.37) |
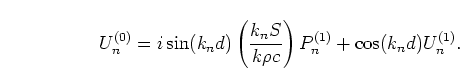 |
(2.38) |
Here 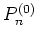 and
and 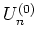 are the complex amplitudes of the pressure
and volume velocity of the
are the complex amplitudes of the pressure
and volume velocity of the  th mode on plane 0 and
th mode on plane 0 and 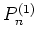 and
and
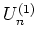 are the complex amplitudes of the pressure and volume velocity
of the
are the complex amplitudes of the pressure and volume velocity
of the  th mode on plane 1 with the planes separated by a distance
th mode on plane 1 with the planes separated by a distance 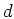 (see figure 2.1).
(see figure 2.1).
We define the pressure vector, 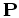 , as a column vector consisting of
the modal pressure amplitudes
, as a column vector consisting of
the modal pressure amplitudes 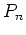 and
and
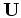 as a column vector of the corresponding
as a column vector of the corresponding 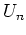 values.
A method of projecting the pressure and velocity vectors along a uniform
section of tube will now be discussed.
values.
A method of projecting the pressure and velocity vectors along a uniform
section of tube will now be discussed.
In matrix notation the pressure vector on plane 0 is given in terms of the
vectors on plane 1 by
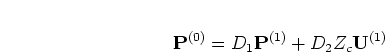 |
(2.39) |
where  ,
, 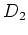 and
and 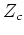 are diagonal matrices with the elements given by
are diagonal matrices with the elements given by
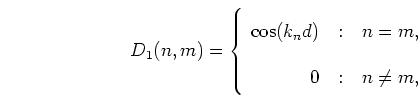 |
(2.40) |
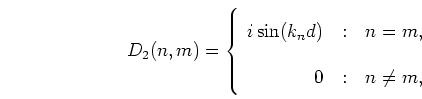 |
(2.41) |
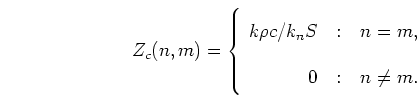 |
(2.42) |
Similarly the volume velocity on plane 0 is given in terms of the vectors
on plane 1 as
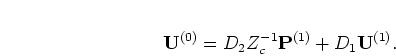 |
(2.43) |
Subsections
Back to Kemp Acoustics Home




Next: Solutions for a cylinder
Up: Multimodal propagation in acoustic
Previous: Plane waves at a
Contents
Jonathan Kemp
2003-03-24
![]() axis and an integer number of nodal lines parallel to the
axis and an integer number of nodal lines parallel to the ![]() axis.
We will only treat systems that preserve symmetry about the central axis, so
only modes with an even number of nodal lines in both dimensions need to be
considered and the subscript
axis.
We will only treat systems that preserve symmetry about the central axis, so
only modes with an even number of nodal lines in both dimensions need to be
considered and the subscript ![]() will be used where
there are
will be used where
there are ![]() nodal lines parallel to the
nodal lines parallel to the ![]() axis and
axis and ![]() nodal lines
parallel to the
nodal lines
parallel to the ![]() axis.
axis.

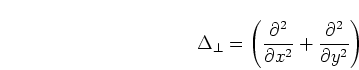
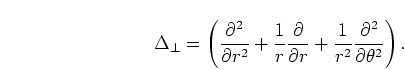
![]() being unity, and so the
being unity, and so the ![]() contribution represents plane wave propagation
while the other modes have a non-uniform pressure profile. Substituting
contribution represents plane wave propagation
while the other modes have a non-uniform pressure profile. Substituting
![]() from equation (2.26) into the wave
equation (2.22) and dividing through by
from equation (2.26) into the wave
equation (2.22) and dividing through by ![]() gives:
gives:
![]() is positive and real above cut-off
point (
is positive and real above cut-off
point (
![]() ) so the pressure varies sinusoidally along the
) so the pressure varies sinusoidally along the ![]() axis
with a wavelength of
axis
with a wavelength of
![]() where
where
![]() is the
free-space wavelength.
Below the cut-off point
is the
free-space wavelength.
Below the cut-off point ![]() is negative and imaginary [42]
so the pressure will be exponentially damped. Calculation of
is negative and imaginary [42]
so the pressure will be exponentially damped. Calculation of ![]() first requires calculation of
first requires calculation of ![]() which in turn
depends on the boundary conditions in equation (2.31)
(and therefore on the geometry of the duct). It will
be treated for both lossy and non-lossy propagation in section
2.4.1 for ducts of circular cross-section and in section
2.4.2 for rectangular ducts.
which in turn
depends on the boundary conditions in equation (2.31)
(and therefore on the geometry of the duct). It will
be treated for both lossy and non-lossy propagation in section
2.4.1 for ducts of circular cross-section and in section
2.4.2 for rectangular ducts.
![]() axis becomes
axis becomes ![]() for the
for the ![]() th mode and, as discussed earlier in the
section, the characteristic
impedance of the
th mode and, as discussed earlier in the
section, the characteristic
impedance of the ![]() th mode is
th mode is
![]() .
Projection of pressure and volume velocity complex amplitudes
of the
.
Projection of pressure and volume velocity complex amplitudes
of the ![]() th mode then follow from equations (2.10) and (2.11).
th mode then follow from equations (2.10) and (2.11).
![]() , as a column vector consisting of
the modal pressure amplitudes
, as a column vector consisting of
the modal pressure amplitudes ![]() and
and
![]() as a column vector of the corresponding
as a column vector of the corresponding ![]() values.
A method of projecting the pressure and velocity vectors along a uniform
section of tube will now be discussed.
values.
A method of projecting the pressure and velocity vectors along a uniform
section of tube will now be discussed.