Back to Kemp Acoustics Home



Next: Lossy propagation
Up: Solutions for a uniform
Previous: Solutions for a uniform
Contents
The boundary condition for the eigenfunction of the 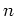 th higher mode
defined in equation (2.31) is:
th higher mode
defined in equation (2.31) is:
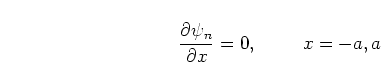 |
(2.63) |
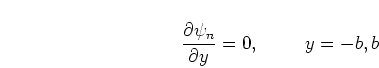 |
(2.64) |
The solution is most conveniently expressed by separating it into the
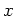 dependent and
dependent and 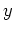 dependent parts:
dependent parts:
 |
(2.65) |
where
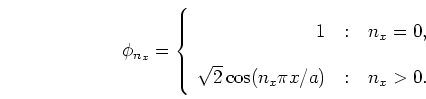 |
(2.66) |
 |
(2.67) |
Performing the differentiation from equation (2.31)
gives the corresponding eigenvalues as
 |
(2.68) |
As with circular cross-section it is possible to use a lossy boundary
condition to give lossy versions of  and
and  but the
effect of losses will be noticeable in the
but the
effect of losses will be noticeable in the 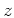 direction only and
will therefore be represented entirely by the choice of
direction only and
will therefore be represented entirely by the choice of 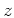 direction
wavenumber,
direction
wavenumber, 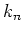 .
.
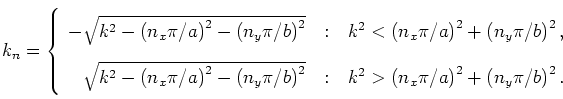 |
(2.69) |
Back to Kemp Acoustics Home



Next: Lossy propagation
Up: Solutions for a uniform
Previous: Solutions for a uniform
Contents
Jonathan Kemp
2003-03-24
![]() th higher mode
defined in equation (2.31) is:
th higher mode
defined in equation (2.31) is:
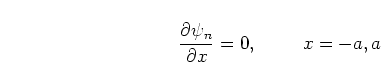
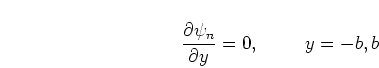

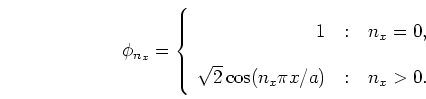
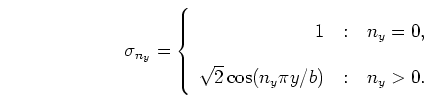
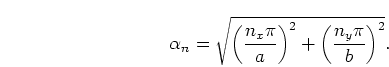
![]() and
and ![]() but the
effect of losses will be noticeable in the
but the
effect of losses will be noticeable in the ![]() direction only and
will therefore be represented entirely by the choice of
direction only and
will therefore be represented entirely by the choice of ![]() direction
wavenumber,
direction
wavenumber, ![]() .
.