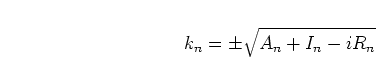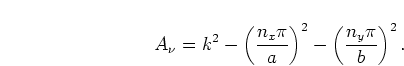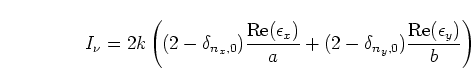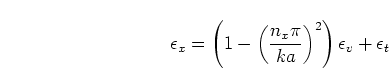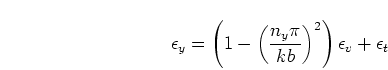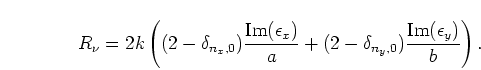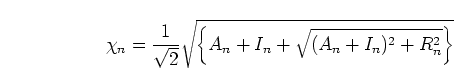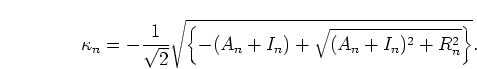Back to Kemp Acoustics Home




Next: Multimodal equations at a
Up: Solutions for a uniform
Previous: Loss-less propagation
Contents
Lossy propagation may be represented as with
circular cross-section by working
out the lossy 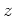 direction wavenumber, (Bruneau et al [44]).
Starting from the lossy boundary condition gives
direction wavenumber, (Bruneau et al [44]).
Starting from the lossy boundary condition gives 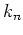 as
as
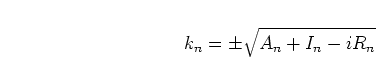 |
(2.70) |
where 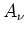 is the square of the non-lossy version of
is the square of the non-lossy version of 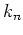 which in
rectangular geometry is
which in
rectangular geometry is
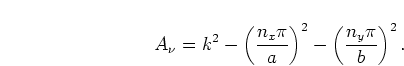 |
(2.71) |
The real part of the correction to 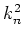 is [44]
is [44]
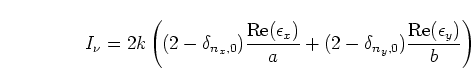 |
(2.72) |
where the boundary specific admittances are
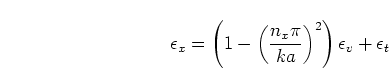 |
(2.73) |
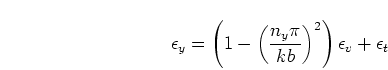 |
(2.74) |
with
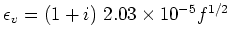 and
and
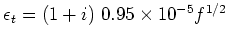 .
The imaginary part of the correction to
.
The imaginary part of the correction to 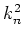 is [44]
is [44]
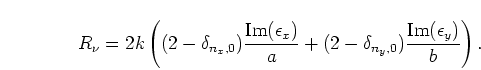 |
(2.75) |
Using the same method as for cylindrical geometry, 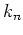 is the sum of real
and imaginary parts
is the sum of real
and imaginary parts
 |
(2.76) |
where 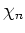 and
and 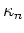 are given by
are given by
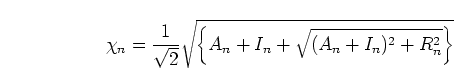 |
(2.77) |
and
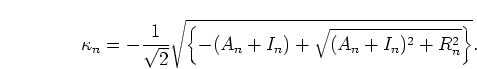 |
(2.78) |
Back to Kemp Acoustics Home




Next: Multimodal equations at a
Up: Solutions for a uniform
Previous: Loss-less propagation
Contents
Jonathan Kemp
2003-03-24
![]() direction wavenumber, (Bruneau et al [44]).
Starting from the lossy boundary condition gives
direction wavenumber, (Bruneau et al [44]).
Starting from the lossy boundary condition gives ![]() as
as