Solutions for a cylinder

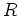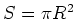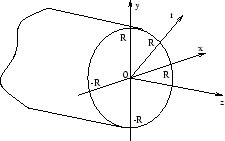
In this section we will show the solutions of the wave equation for pipes of uniform cross-section. Consider a cylinder of radius $R$ (cross-sectional area is $S=\pi R^2$) as shown in figure 2.3.

Figure 2.3: Cylindrical waveguide with radius 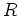$R$

First we will examine the case of loss-less propagation along a duct of infinitely hard walls. No flow is allowed through the walls so the gradient of the pressure along the radial direction must equal zero at the wall. This boundary condition will be used to derive expressions for the mode profiles on the x-y plane, and the corresponding wavenumbers along the different dimensions. The modes in a uniform cylindrical duct will then be illustrated in a colour pressure map. We then go on to show the solutions for lossy propagation.

The profile of the various modes are the eigenfunctions defined in equation (2.31). In general, the solution need not be axially symmetric. Musical wind instruments are, however, generally designed so that the internal profile has no sharp sideways steps and only feature relatively gradual bends. This means that the behaviour may be modelled accurately by approximating the profile by a series of concentric cylinders. Only axially symmetric modes will have an effect on the response of an instrument assuming the excitation is also axi-symmetric. The present discussion will therefore be limited to axi-symmetric modes only. This approximation ignores the fact that the excitation from a brass instrument player's lips is not perfectly axially symmetric.