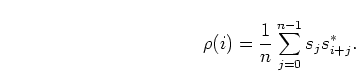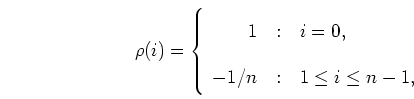Back to Kemp Acoustics Home



Next: Extracting the system impulse
Up: Maximum length sequences
Previous: Generating an MLS sequence
Contents
In order to use an MLS in a measurement, it is preferable to convert the
signal to one which oscillates around zero rather than above zero because
this reduces the dc offset and therefore improves the efficiency of
loudspeakers and measurement systems. This can be done by defining
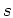 as a sequence obtained by replacing every 0 with 1 and replacing
every 1 with -1 as follows:
as a sequence obtained by replacing every 0 with 1 and replacing
every 1 with -1 as follows:
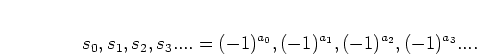 |
(7.4) |
The auto-correlation function, 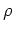 , is defined as [68]
, is defined as [68]
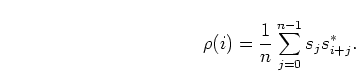 |
(7.5) |
where 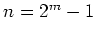 is the length of the sequence. Note that the subscript
is the length of the sequence. Note that the subscript 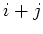 can exceed
can exceed 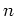 . When this happens the subscript is taken modulo
. When this happens the subscript is taken modulo 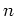 (ie.
(ie. 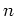 is
subtracted so that
is
subtracted so that 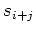 is a circularly shifted version of
is a circularly shifted version of 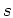 ).
The symbol * denotes complex conjugation which may be dropped in the current
application because all entries in the sequence are real.
).
The symbol * denotes complex conjugation which may be dropped in the current
application because all entries in the sequence are real.
For the MLS defined in equation (7.4), the auto-correlation becomes:
 |
(7.6) |
where 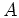 is the number of times the elements
is the number of times the elements
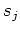 and
and 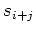 agree and
agree and 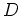 is the number of times they disagree.
The first term in
is the number of times they disagree.
The first term in 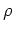 is given by
is given by 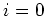 so
so 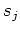 and
and 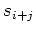 agree
for all values of
agree
for all values of 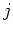 giving
giving 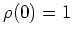 . When
. When
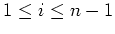 we are
calculating the agreement between the signal and a circularly shifted version.
Since the signals appear random, it is intuitive that the agreement and
disagreement should be almost equal. The proof in [68] shows that
we are
calculating the agreement between the signal and a circularly shifted version.
Since the signals appear random, it is intuitive that the agreement and
disagreement should be almost equal. The proof in [68] shows that
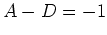 for
for
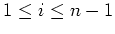 . The auto-correlation of the MLS is therefore
. The auto-correlation of the MLS is therefore
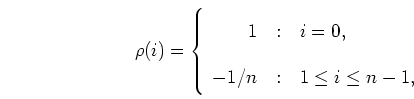 |
(7.7) |
which is distinguished from a perfect digital impulse by the presence of
the small non-zero value when 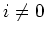 . While the frequency spectrum of an
ideal digital impulse is equal for all frequencies,
the frequency spectrum of
. While the frequency spectrum of an
ideal digital impulse is equal for all frequencies,
the frequency spectrum of  is the same for all frequencies except for
the zero frequency component.
is the same for all frequencies except for
the zero frequency component.
Back to Kemp Acoustics Home



Next: Extracting the system impulse
Up: Maximum length sequences
Previous: Generating an MLS sequence
Contents
Jonathan Kemp
2003-03-24
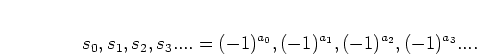
![]() , is defined as [68]
, is defined as [68]