Back to Kemp Acoustics Home




Next: Results
Up: Multimodal radiation impedance of
Previous: Multimodal radiation impedance of
Contents
Consider a rectangular duct of half widths 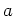 and
and 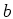 terminated in an
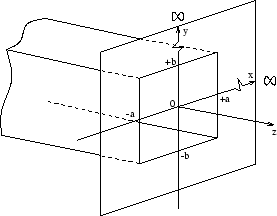
infinite baffle, as shown in figure 3.4.
terminated in an
infinite baffle, as shown in figure 3.4.
Figure 3.4:
Geometry of infinitely flanged rectangular duct
 |
Expressing (3.13) in rectangular coordinates for a rectangular duct
of half-widths 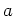 and
and 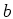 gives:
gives:
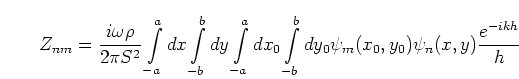 |
(3.26) |
where
![\begin{displaymath}
h = [(x-x_0)^2 + (y-y_0)^2]^{\frac{1}{2}},
\end{displaymath}](img381.png) |
(3.27) |
and
 |
(3.28) |
with
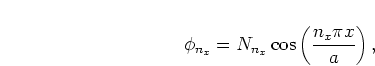 |
(3.29) |
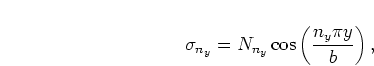 |
(3.30) |
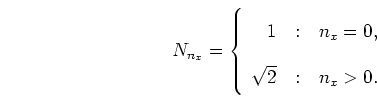 |
(3.31) |
Changing variables as in Swenson et al. [49] and Levine [51] to
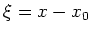 ,
,
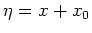 ,
,
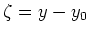 , and
, and 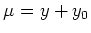 the integral becomes
the integral becomes
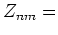 |
| |
|
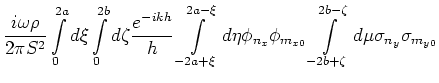 |
|
| |
|
|
(3.32) |
where
 |
(3.33) |
The quadruple integral can now be reduced to a double integral
by performing integration by 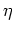 and
and 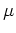 analytically.
The first step is to expand the cosines in equations (3.29)
and (3.30):
analytically.
The first step is to expand the cosines in equations (3.29)
and (3.30):
The second and third terms go to zero
since we are integrating over a symmetric interval in 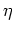 .
Performing integration gives:
.
Performing integration gives:
The integral for the impedance is then:
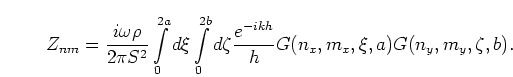 |
(3.36) |
Changing variables to 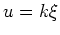 and
and 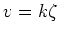 means that the radiation
impedance is expressed in terms of the dimensionless variables
means that the radiation
impedance is expressed in terms of the dimensionless variables 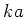 and
and 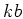 :
:
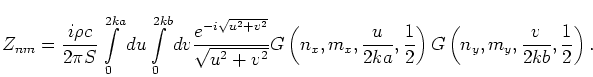 |
(3.37) |
Note that if we put
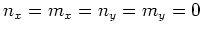 into equation
(3.35) we obtain
into equation
(3.35) we obtain
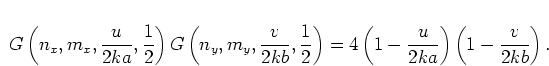 |
(3.38) |
The radiation impedance from equation (3.37) is then identical to
the radiation impedance of a rectangular piston in an
infinite baffle [47,48,49,50,51] (note that most authors
have used 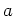 and
and 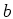 as widths rather than half widths). Equation
(3.37) has a singularity at the origin if
as widths rather than half widths). Equation
(3.37) has a singularity at the origin if 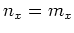 and
and 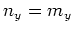 which must be removed if the radiation impedance is to be calculated by
numerical integration. To do this the integral is first split into two parts:
which must be removed if the radiation impedance is to be calculated by
numerical integration. To do this the integral is first split into two parts:
where
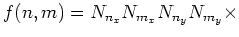 |
| |
|
![$\displaystyle \left[{\mathrm sinc}((n_x+m_x)\pi)
+ {\mathrm sinc}((n_x-m_x)\pi)\right]
\left[{\mathrm sinc}((n_y+m_y)\pi)
+ {\mathrm sinc}((n_y-m_y)\pi)\right].$](img415.png) |
|
| |
|
|
(3.40) |
The first part is non-singular and the singularity in the second half may be
removed by integration, giving:
Equation (3.41) may be evaluated by numerical integration to
provide the radiation impedance.
Back to Kemp Acoustics Home




Next: Results
Up: Multimodal radiation impedance of
Previous: Multimodal radiation impedance of
Contents
Jonathan Kemp
2003-03-24
![]() and
and ![]() terminated in an
infinite baffle, as shown in figure 3.4.
terminated in an
infinite baffle, as shown in figure 3.4.
![]() and
and ![]() gives:
gives:
![\begin{displaymath}
h = [(x-x_0)^2 + (y-y_0)^2]^{\frac{1}{2}},
\end{displaymath}](img381.png)

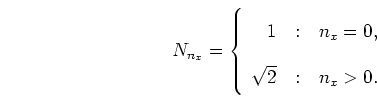
![]() ,
,
![]() ,
,
![]() , and
, and ![]() the integral becomes
the integral becomes
![]() and
and ![]() means that the radiation
impedance is expressed in terms of the dimensionless variables
means that the radiation
impedance is expressed in terms of the dimensionless variables ![]() and
and ![]() :
: