Back to Kemp Acoustics Home



Next: Multimodal radiation impedance of
Up: Radiation impedance
Previous: Pressure radiation from a
Contents
In chapter 2 we defined the acoustic impedance in a
duct as the ratio of the pressure amplitude to the volume velocity amplitude.
We therefore wish to define the radiation impedance as the ratio of the
pressure amplitude and the volume velocity amplitude on the radiating surface.
An expression has been derived for the total pressure field in terms of the
volume velocity amplitude. The next step is therefore to calculate
the pressure amplitude of a particular mode at 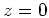 from the total pressure field.
To do this we first express the pressure field there as the sum of the
contributions of all the modes,
from the total pressure field.
To do this we first express the pressure field there as the sum of the
contributions of all the modes,
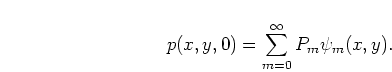 |
(3.6) |
Now we recall the orthogonality of the modes from
equation (2.47):
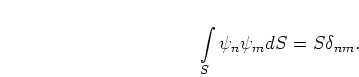 |
(3.7) |
Multiplying 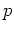 by
by 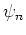 and integrating over the surface area therefore
gives
and integrating over the surface area therefore
gives
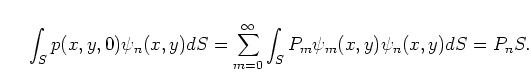 |
(3.8) |
When this is rearranged, the pressure amplitude of the 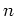 th mode is given
in terms of the total pressure field as
th mode is given
in terms of the total pressure field as
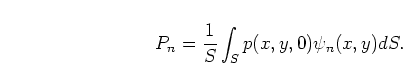 |
(3.9) |
Now we will work out how the pressure and velocity modes couple.
Substituting equation (3.5), which gives the total pressure field due
to the contribution of the velocity modes, into equation (3.9)
gives
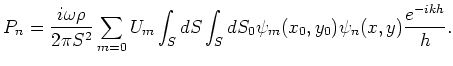 |
|
|
(3.10) |
This expression gives the pressure amplitude of the 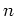 th
mode due to the contributions of all the velocity modes,
not just the
th
mode due to the contributions of all the velocity modes,
not just the 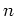 th velocity mode. The modes are therefore coupled at the
opening as was expected.
th velocity mode. The modes are therefore coupled at the
opening as was expected.
Looking back to equation (2.95), the relationship between the pressure
and velocity modes was given as
 |
(3.11) |
where 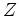 is known as the impedance matrix.
is known as the impedance matrix. 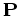 is the column
vector whose
is the column
vector whose 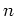 th element is the pressure amplitude of the
th element is the pressure amplitude of the 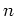 th mode,
th mode, 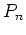 .
Similarly,
.
Similarly, 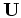 is the column vector whose
is the column vector whose 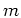 th element is the
volume velocity amplitude of the
th element is the
volume velocity amplitude of the 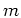 th mode,
th mode, 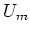 . Expressing this in
summation notation, we get
. Expressing this in
summation notation, we get
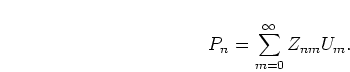 |
(3.12) |
Comparison of equations (3.10) and (3.12) yields
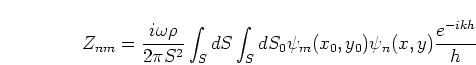 |
(3.13) |
where 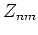 is the
is the 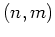 element of the impedance matrix and gives the
contribution to the
element of the impedance matrix and gives the
contribution to the 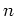 th pressure mode by the
th pressure mode by the 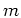 th velocity mode.
Because this is the impedance at the open end, we call the impedance matrix
here the ``radiation impedance matrix''.
Note that we are integrating twice: first we integrate to get the pressure
field at
th velocity mode.
Because this is the impedance at the open end, we call the impedance matrix
here the ``radiation impedance matrix''.
Note that we are integrating twice: first we integrate to get the pressure
field at 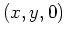 due to the sum of all source elements and then we integrate this
pressure at every point in the piston to isolate a single modal pressure
amplitude component.
due to the sum of all source elements and then we integrate this
pressure at every point in the piston to isolate a single modal pressure
amplitude component.
Back to Kemp Acoustics Home



Next: Multimodal radiation impedance of
Up: Radiation impedance
Previous: Pressure radiation from a
Contents
Jonathan Kemp
2003-03-24
![]() from the total pressure field.
To do this we first express the pressure field there as the sum of the
contributions of all the modes,
from the total pressure field.
To do this we first express the pressure field there as the sum of the
contributions of all the modes,