Back to Kemp Acoustics Home




Next: Projection matrix in cylindrical
Up: General expression
Previous: Pressure
Contents
In plane wave propagation the continuity condition was that the volume
velocity must be equal on 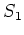 and
and 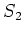 meaning that the
mass of air flowing out of
meaning that the
mass of air flowing out of 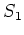 equals the flow of mass into
equals the flow of mass into 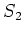 at any
given time. This implies that the velocity, which is assumed to be constant
over the cross-section, is different on either side because of the
difference of cross-sectional area. When we are treating the
velocity field accurately in three dimensions it is clear that the
velocity on the two surfaces should match and that the velocity into the
at any
given time. This implies that the velocity, which is assumed to be constant
over the cross-section, is different on either side because of the
difference of cross-sectional area. When we are treating the
velocity field accurately in three dimensions it is clear that the
velocity on the two surfaces should match and that the velocity into the
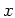 -
-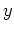 plane wall on the larger cross-section is zero. For the
case where
plane wall on the larger cross-section is zero. For the
case where 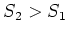 we have
we have
where  is a shorthand for the
is a shorthand for the 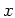 -
-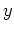 plane wall resulting
from the part of surface 2 which is not shared with surface 1.
In terms of volume velocities this means that
plane wall resulting
from the part of surface 2 which is not shared with surface 1.
In terms of volume velocities this means that
 on
on 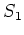 and
and  on
on  .
Now we will use equation (2.27) (again ignoring the
.
Now we will use equation (2.27) (again ignoring the
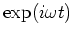 time factor) and use the orthogonality of the
modes. This time in order to include the fact that the volume velocity is
zero on
time factor) and use the orthogonality of the
modes. This time in order to include the fact that the volume velocity is
zero on  we must perform the integration over surface 2:
we must perform the integration over surface 2:
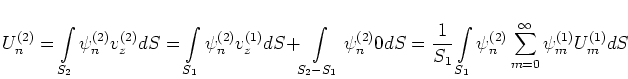 |
(B.11) |
which may be written as
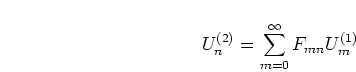 |
(B.12) |
where 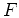 is given in equation (B.6). It should be noted
that the integration in
is given in equation (B.6). It should be noted
that the integration in 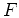 is this time over
the
is this time over
the  on surface 1 and over
on surface 1 and over 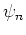 on surface 2, hence
on surface 2, hence 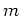 and
and  in the subscript to
in the subscript to 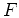 are swapped for equation (B.12). In
matrix notation the result is
are swapped for equation (B.12). In
matrix notation the result is
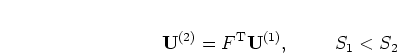 |
(B.13) |
proving equation (2.83). The swapping of indices in 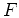 is denoted
by the transpose operation represented by the superscript
is denoted
by the transpose operation represented by the superscript  .
.
As with the pressure, when 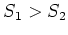 the volume velocity calculation
can be performed simply be interchanging the labels 1 and 2 giving
equation (2.84):
the volume velocity calculation
can be performed simply be interchanging the labels 1 and 2 giving
equation (2.84):
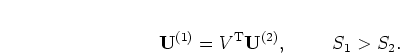 |
(B.14) |
with 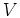 given in equation (B.9).
given in equation (B.9).
Back to Kemp Acoustics Home




Next: Projection matrix in cylindrical
Up: General expression
Previous: Pressure
Contents
Jonathan Kemp
2003-03-24
![]() and
and ![]() meaning that the
mass of air flowing out of
meaning that the
mass of air flowing out of ![]() equals the flow of mass into
equals the flow of mass into ![]() at any
given time. This implies that the velocity, which is assumed to be constant
over the cross-section, is different on either side because of the
difference of cross-sectional area. When we are treating the
velocity field accurately in three dimensions it is clear that the
velocity on the two surfaces should match and that the velocity into the
at any
given time. This implies that the velocity, which is assumed to be constant
over the cross-section, is different on either side because of the
difference of cross-sectional area. When we are treating the
velocity field accurately in three dimensions it is clear that the
velocity on the two surfaces should match and that the velocity into the
![]() -
-![]() plane wall on the larger cross-section is zero. For the
case where
plane wall on the larger cross-section is zero. For the
case where ![]() we have
we have
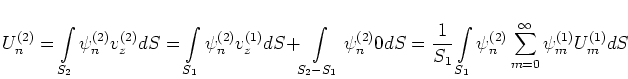
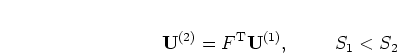
![]() the volume velocity calculation
can be performed simply be interchanging the labels 1 and 2 giving
equation (2.84):
the volume velocity calculation
can be performed simply be interchanging the labels 1 and 2 giving
equation (2.84):