Back to Kemp Acoustics Home




Next: Pressure radiation from a
Up: The piston approximation
Previous: The piston approximation
Contents
Pressure radiation from a piston terminated in an infinite baffle
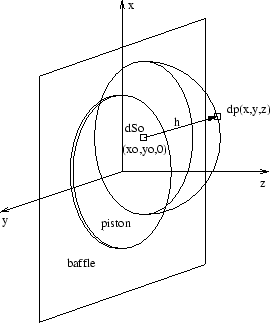
Consider a rigid piston in a rigid infinite baffle as shown in figure
3.1.
The piston vibrates uniformly with a sinusoidal velocity of amplitude 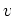 normal to the baffle.
normal to the baffle.
Figure 3.1:
Piston in an infinite baffle
 |
In order to calculate the behaviour of this system, we split the
piston into infinitesimal simple source elements and sum the resulting
pressure fields. A piston
surface element of area 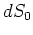 is present at
is present at 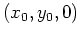 . This
surface element oscillates with a velocity amplitude of
. This
surface element oscillates with a velocity amplitude of 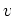 normal to the
baffle and acts as a simple source of spherical pressure waves. These are
represented on the diagram by a hemispherical shell, with the acoustic
pressure at a distance
normal to the
baffle and acts as a simple source of spherical pressure waves. These are
represented on the diagram by a hemispherical shell, with the acoustic
pressure at a distance
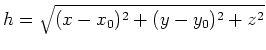 from the
source element given by [40]
from the
source element given by [40]
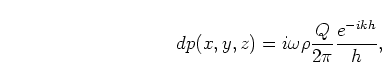 |
(3.2) |
where 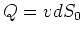 is the simple source
strength and a
is the simple source
strength and a 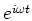 time factor is assumed throughout. The part
time factor is assumed throughout. The part
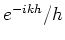 is known as the Green's function and implies that the
pressure oscillates sinusoidally in space with wavelength
is known as the Green's function and implies that the
pressure oscillates sinusoidally in space with wavelength
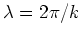 and with an amplitude that dies as
and with an amplitude that dies as 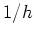 . Integrating
(3.2) over
. Integrating
(3.2) over 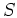 , the surface of the whole piston, we get the
total pressure field due to the sum of all the source elements that make up
the piston.
, the surface of the whole piston, we get the
total pressure field due to the sum of all the source elements that make up
the piston.
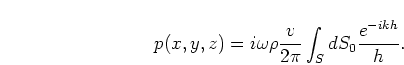 |
(3.3) |
Note that the integrand is singular (tends to infinity) as 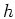 tends to zero.
This problem must be addressed before numerical integration
is possible.
tends to zero.
This problem must be addressed before numerical integration
is possible.
Back to Kemp Acoustics Home




Next: Pressure radiation from a
Up: The piston approximation
Previous: The piston approximation
Contents
Jonathan Kemp
2003-03-24
![]() normal to the baffle.
normal to the baffle.
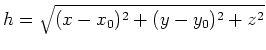 from the
source element given by [40]
from the
source element given by [40]