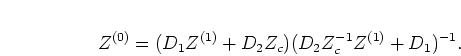 |
(2.99) |
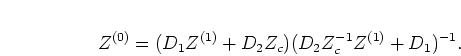 |
(2.99) |
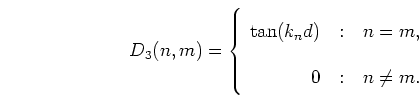 |
(2.101) |
The input impedance matrix may then be calculated from the output end impedance matrix by projecting alternately along a cylinder using equation (2.100) and across a discontinuity using equation (2.97) until the input end is reached.
Typically the acoustic horns that we will consider are cylindrical at the input end and only flare out towards the open end. The radiation impedance matrix at an open end is the subject of the next chapter. A waveguide terminated in an infinite cylindrical pipe is also a useful subject of theoretical study. In such an infinite terminating pipe all waves are forward going and the impedance is simply given by the characteristic impedance matrix of equation (2.42).