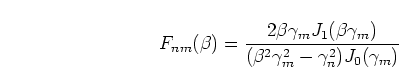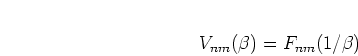Back to Kemp Acoustics Home




Next: Solutions for rectangular cross-section
Up: Multimodal equations at a
Previous: Multimodal equations at a
Contents
The matrices  and
and  defined in (2.80) can be found
analytically for circular cross-section using the standard integral in
equation (A.1) of appendix A.
A full derivation is given in appendix B.
The result is that each element is a
function of
defined in (2.80) can be found
analytically for circular cross-section using the standard integral in
equation (A.1) of appendix A.
A full derivation is given in appendix B.
The result is that each element is a
function of
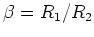 and the element
and the element 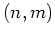 is given by
is given by
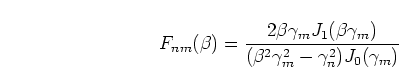 |
(2.85) |
where 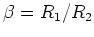 and
and 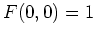 and
and
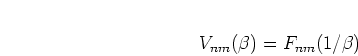 |
(2.86) |
When the change in cross-section tends to zero (ie. 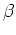 tends to 1)
we obtain
tends to 1)
we obtain
 |
(2.87) |
with 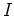 being the identity matrix (a diagonal matrix with all the entries
having a value of 1).
being the identity matrix (a diagonal matrix with all the entries
having a value of 1). 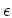 is the fractional change in cross-section,
is the fractional change in cross-section,
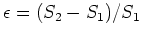 and
and 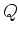 is a matrix whose
elements are given by
is a matrix whose
elements are given by
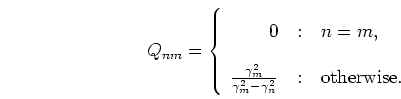 |
(2.88) |
Back to Kemp Acoustics Home




Next: Solutions for rectangular cross-section
Up: Multimodal equations at a
Previous: Multimodal equations at a
Contents
Jonathan Kemp
2003-03-24