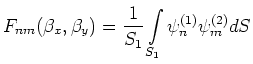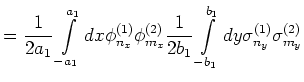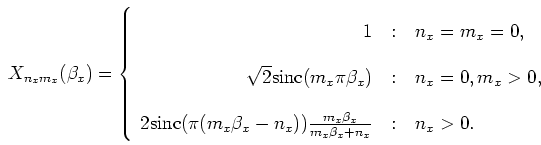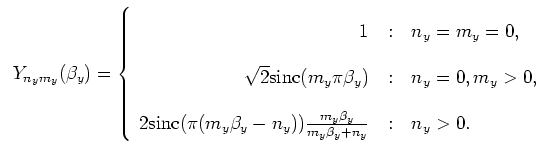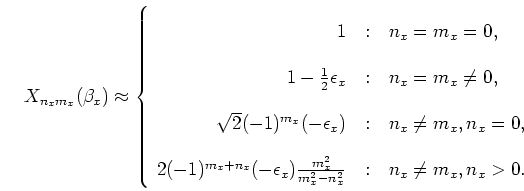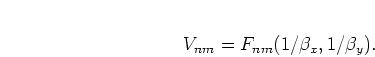Back to Kemp Acoustics Home



Next: Method for calculation of
Up: Multimodal equations at a
Previous: Solutions for circular cross-section
Contents
The 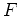 matrix defined in (2.80) may be presented most
conveniently in rectangular coordinates by expressing each entry as the
multiplication of two terms:
matrix defined in (2.80) may be presented most
conveniently in rectangular coordinates by expressing each entry as the
multiplication of two terms:
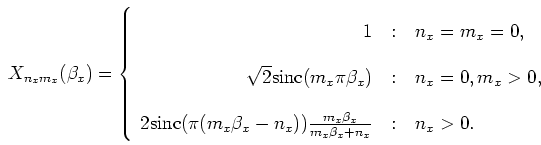 |
(2.90) |
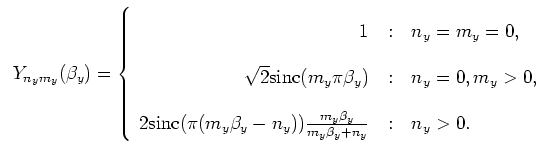 |
(2.91) |
where
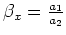 and
and
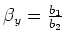 .
When both
.
When both 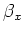 and
and 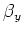 tend to 1 we get
tend to 1 we get
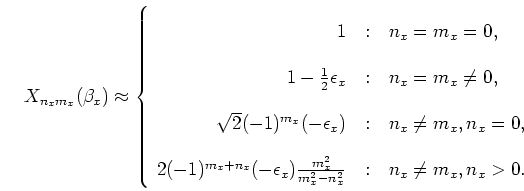 |
(2.92) |
 |
(2.93) |
where
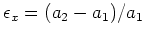 and
and
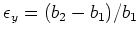 .
The
.
The 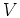 matrix will have entries given by
matrix will have entries given by
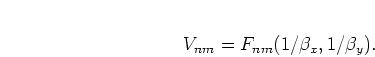 |
(2.94) |
Back to Kemp Acoustics Home



Next: Method for calculation of
Up: Multimodal equations at a
Previous: Solutions for circular cross-section
Contents
Jonathan Kemp
2003-03-24
![]() matrix defined in (2.80) may be presented most
conveniently in rectangular coordinates by expressing each entry as the
multiplication of two terms:
matrix defined in (2.80) may be presented most
conveniently in rectangular coordinates by expressing each entry as the
multiplication of two terms: