Back to Kemp Acoustics Home



Next: The piston approximation
Up: Radiation impedance
Previous: Introduction
Contents
A first approximation to the behaviour at the end of a
duct may be obtained using the plane wave approximation.
Recalling equation (2.20), the plane wave
approximation reflection coefficient at a change in cross-section from
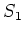 to
to 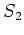 is given by:
is given by:
 |
(3.1) |
An open end corresponds to 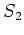 tending to infinity, so
tending to infinity, so 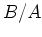 tends to -1.
The acoustic wave is reflected back down the duct
tends to -1.
The acoustic wave is reflected back down the duct 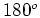 out of
phase implying standing waves with zero pressure amplitude at the open end
as mentioned in chapter 1.
While this is useful for obtaining a first approximation for the behaviour
of musical instruments it is obvious that, even ignoring mode conversion at
the opening for the moment, a more accurate analysis of the
end condition should account for the sound radiated from the end of the
instrument.
out of
phase implying standing waves with zero pressure amplitude at the open end
as mentioned in chapter 1.
While this is useful for obtaining a first approximation for the behaviour
of musical instruments it is obvious that, even ignoring mode conversion at
the opening for the moment, a more accurate analysis of the
end condition should account for the sound radiated from the end of the
instrument.
Jonathan Kemp
2003-03-24
![]() to
to ![]() is given by:
is given by:
